Union Find Algorithm Part 2
It’s been a while, but I’m finally posting the second half of the Union Find algorithm series! I ended the first section with the Quick Union solution. This blog will focus on two improvements to this solution, the weighted Quick Union and weighted Quick Union with Path Compression.
Quick Union Improvement 1: Weighted
The first improvement takes into account the size of the trees. One of the downfalls of Quick Union is that the trees can get very tall, making the find operation very expensive. With the weighted improvement each instance of quick union is initialized with a “size” array that tracks the size of each group. Then in the union method there is a condition that checks which tree is larger before joining them. The root of the smaller tree is always added to the root of the bigger tree, creating a more balanced solution.
class WeightedQuickUnion {
// initialize with an array that shows the size of each group at it's index
constructor(num) {
this.ids = [];
this.size = [];
for (let i = 0; i < num; i++){
this.ids.push(i)
this.size.push(1)
}
}
// root is where ids[i] is same as index
findRoot = (i) => {
while (i !== this.ids[i]) {
i = this.ids[i];
}
return i;
}
union = (p, q) => {
let i = this.findRoot(p);
let j = this.findRoot(q);
if ( i === j) {
return
}
// below we connect the smaller tree to the larger tree and increase the size of the larger tree
if (this.size[i] < this.size[j]) {
this.ids[i] = j;
this.size[j] += this.size[i];
} else {
this.ids[j] = i;
this.size[i] += this.size[j]
}
}
}Above the union function is where the new action takes place–where the root of the smaller tree is altered to point to the root of the larger tree and the size of the larger tree is increased by the size of the smaller tree. In the test code below, imagine an instance of the Weighted Quick Union class with some unions already present. Here’s the code for the instance:
// assume this is where we're starting with an instance of WQU called test:
WeightedQuickUnion {
findRoot: [Function: findRoot],
union: [Function: union],
ids: [
0, 1, 7, 7, 4,
5, 1, 7, 1, 3
],
size: [
1, 3, 1, 2, 1,
1, 1, 4, 1, 1
]
}And a visual:
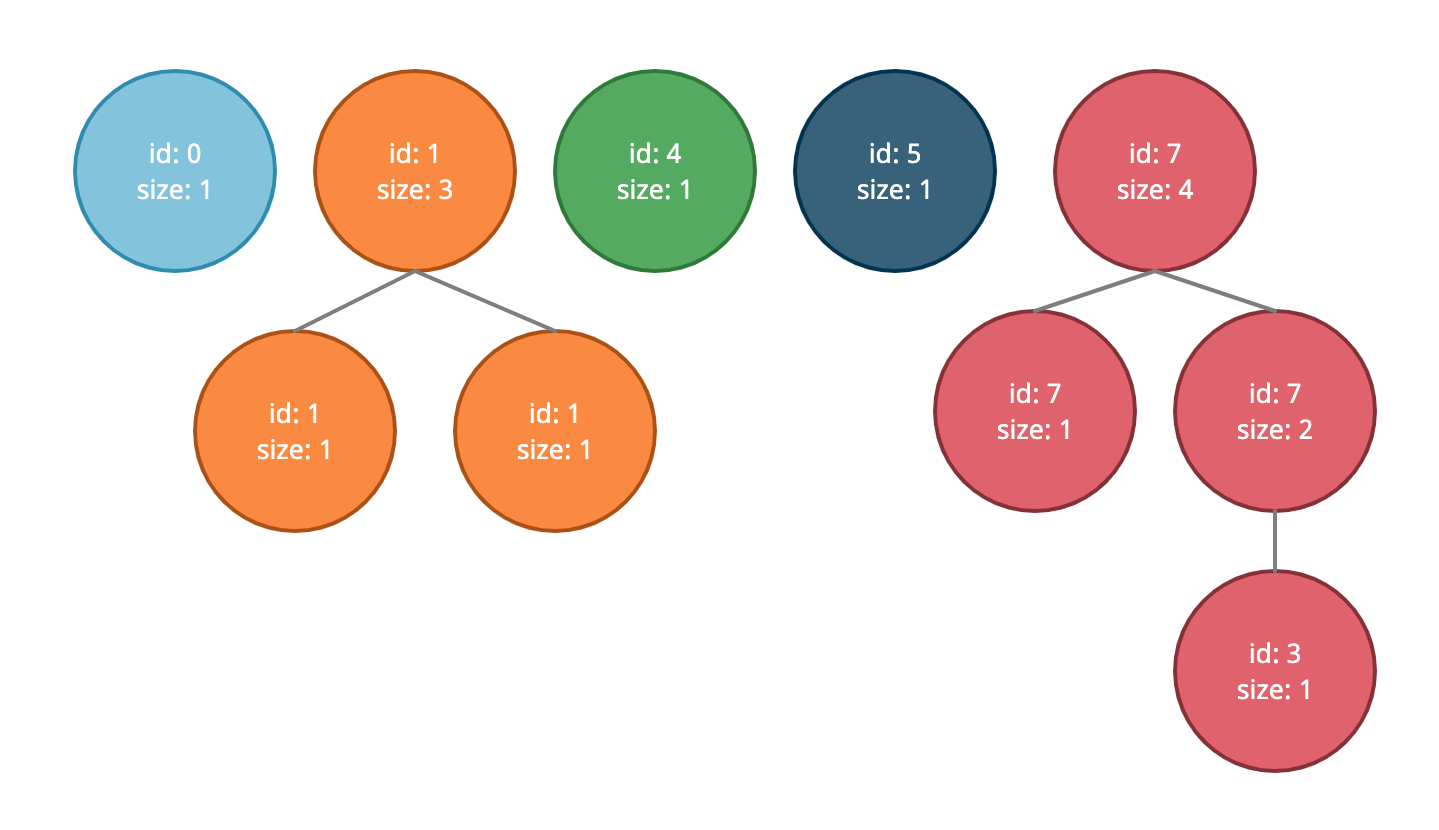
Here we can see that there are 5 separate sets with roots of 0, 1, 4, 5, and 7. Seven is the largest tree with size 4. If we run two unions, one between 4 and 5 and the other between 1 and 7, we’ll see the changes below.
// before the union of 1 and 7
test.union(4, 5)
WeightedQuickUnion {
findRoot: [Function: findRoot],
union: [Function: union],
ids: [
0, 1, 7, 7, 4,
4, 1, 7, 1, 3
],
size: [
1, 3, 1, 2, 2,
1, 1, 4, 1, 1
]
}
test.union(1, 7)
// after the union of 1 and 7
WeightedQuickUnion {
findRoot: [Function: findRoot],
union: [Function: union],
ids: [
0, 7, 7, 7, 4,
4, 1, 7, 1, 3
],
size: [
1, 3, 1, 2, 2,
1, 1, 7, 1, 1
]
}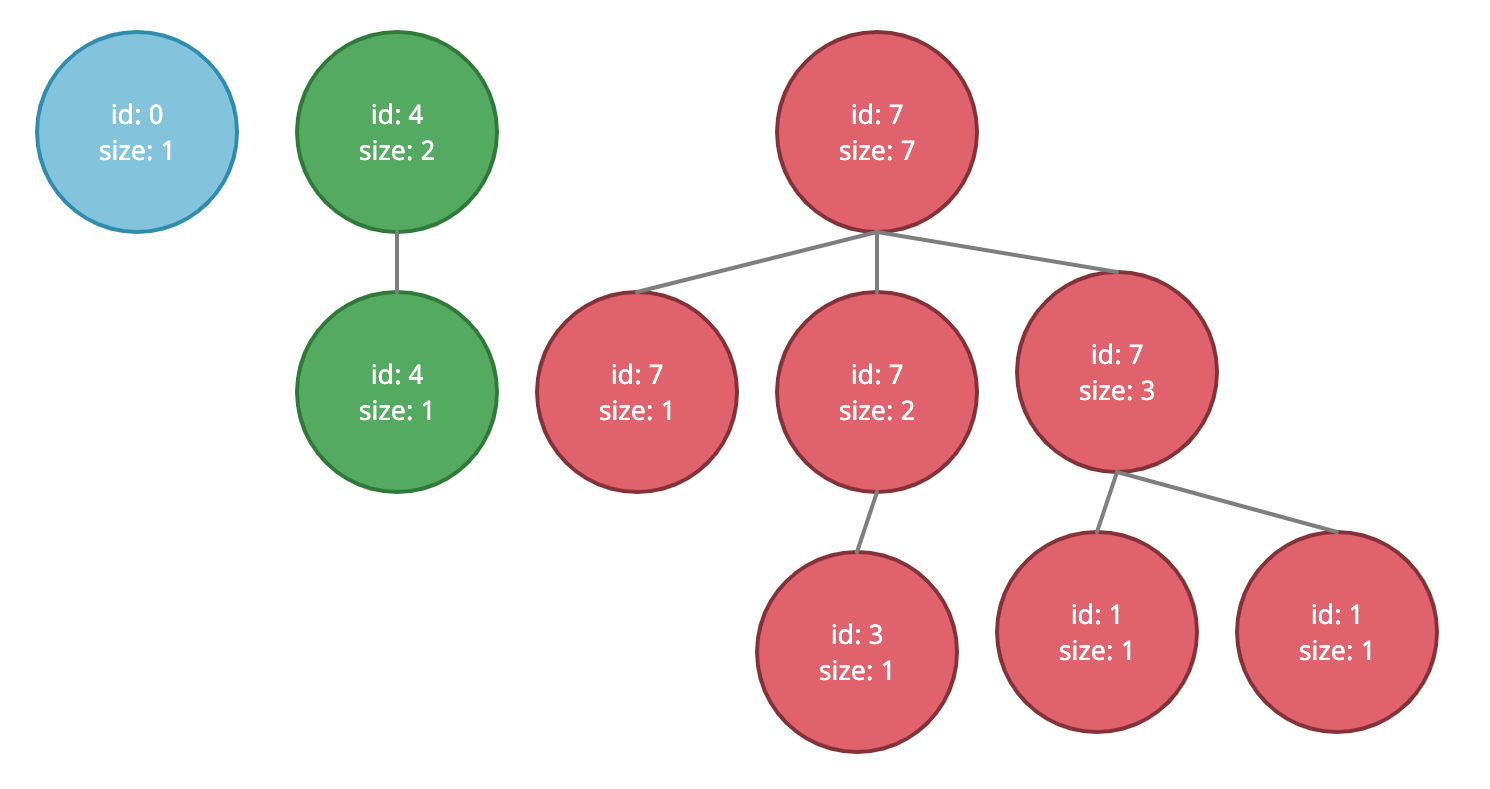
We can see that the smaller tree with root 1 was joined to the larger tree with root 7, making that tree grow to 7. We can continue improving this solution by adding path compression!
Quick Union Improvement 2: Path Compression
This improvement modifies the findRoot method in QuickUnion to compress the path length. This could be done in two passes by finding the root of the provided element and then setting the value of each examined element to that root, which flattens the path. Or it could be done in one pass by setting every other examined element to point directly to its grandparent. This second way halves the path and is a simpler implementation. Here’s the WeightedQuickUnionWithPathCompression class with that modified method:
class WeightedQuickUnionWithPathCompression {
constructor(num) {
this.ids = [];
this.size = [];
for (let i = 0; i < num; i++){
this.ids.push(i)
this.size.push(1)
}
}
// the modified findRoot method
findRoot = (i) => {
while ( i !== this.ids[i]) {
this.ids[i] = this.ids[this.ids[i]];
i = this.ids[i]
}
return i;
}
connected = (p, q) => {
return this.findRoot(p) === this.findRoot(q);
}
union = (p, q) => {
let i = this.findRoot(p);
let j = this.findRoot(q);
if ( i === j) {
return
}
if (this.size[i] < this.size[j]) {
this.ids[i] = j;
this.size[j] += this.size[i];
} else {
this.ids[j] = i;
this.size[i] += this.size[j]
}
}
}Let’s take a look at how the path compression works. If we begin with a class instance that looks like the below:
WeightedQuickUnionWithPathCompression {
findRoot: [Function: findRoot],
connected: [Function: connected],
union: [Function: union],
ids: [
3, 3, 7, 3, 4,
4, 6, 3, 8, 0
],
size: [
2, 1, 1, 6, 2,
1, 1, 2, 1, 1
]
}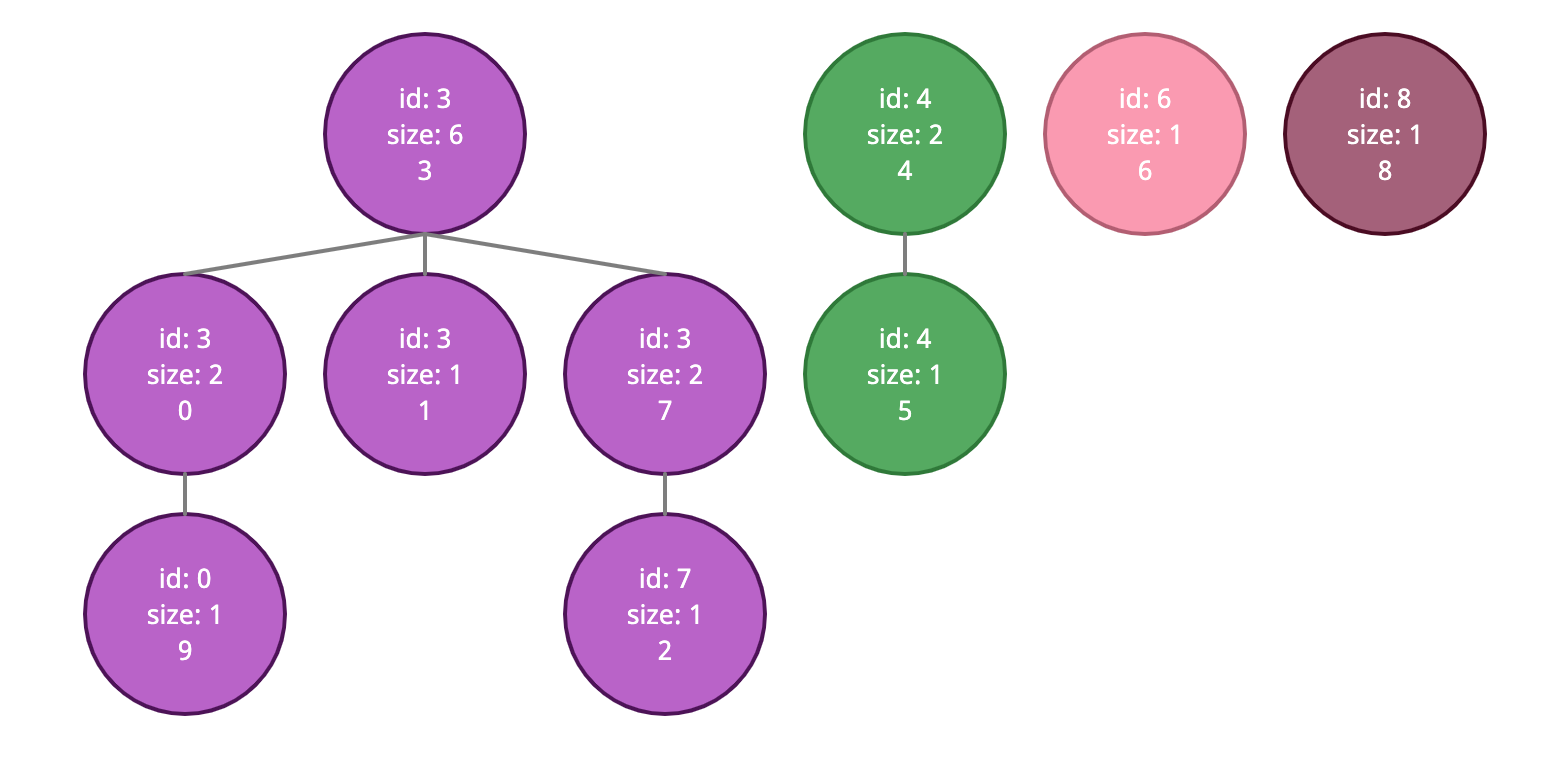
Here we can see that we have 4 root ids, 3, 4, 6, and 8, with sizes 6, 2, 1, and 1, respectively. If we call union between the nodes 4 and 9 (the node numbers are the last line of text in the image and the index numbers in the array), this will join the tree with root 4 to the tree with root 3 and this will alter the id of node 9. Currently node 9 has an id of 0, but after we run the union method 9 will point to its grandparent 3 instead of 0, thereby compressing the path! Let’s take a look:
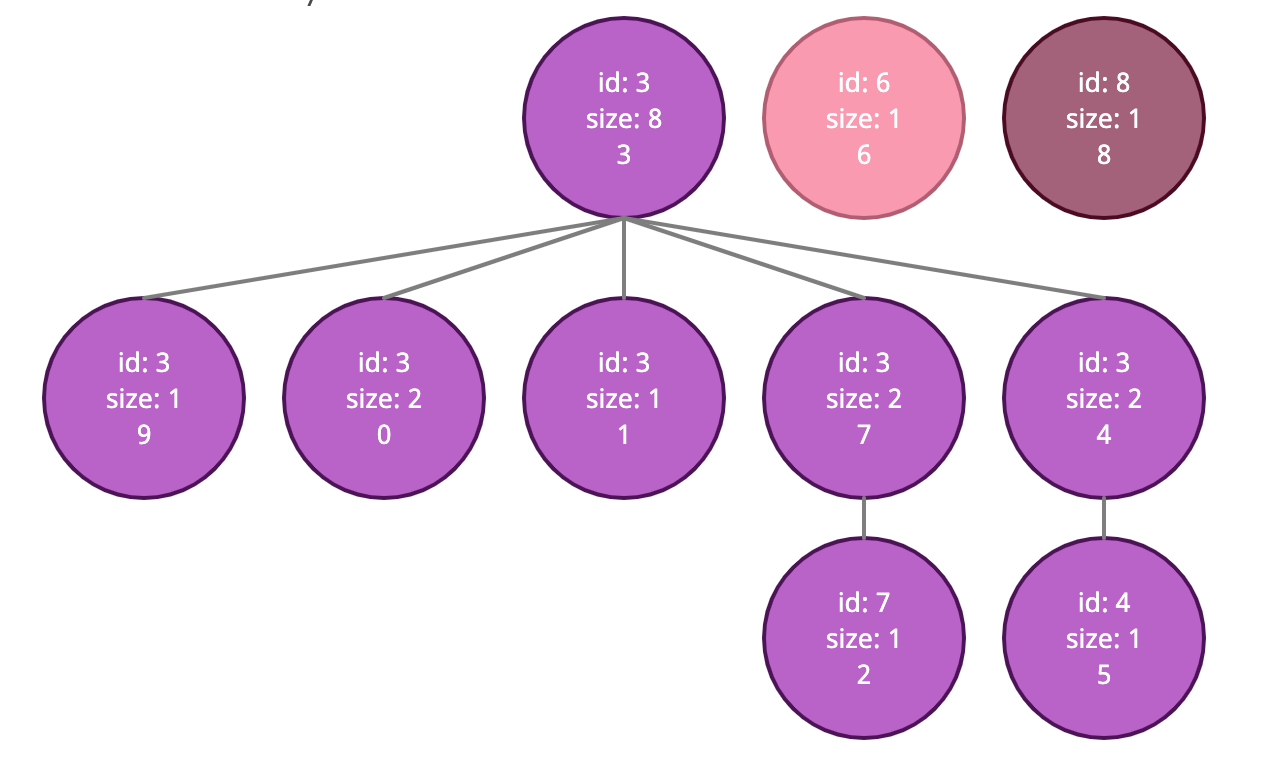
test.union(9, 4)
// last
WeightedQuickUnionWithPathCompression {
findRoot: [Function: findRoot],
connected: [Function: connected],
union: [Function: union],
ids: [
3, 3, 7, 3, 3,
4, 6, 3, 8, 3
],
size: [
2, 1, 1, 8, 2,
1, 1, 2, 1, 1
]
}
The combination of these two improvements take what was a quadratic, unscalable solution (the UnionFind class from part 1) to a linear solution! Check out my source for this series to get more details about uses for this algorithm and more detail about these improvements and the time complexity analysis.
Source: Princeton University, Algorithms Part I, taught by Robert Sedgewick and Kevin Wayne